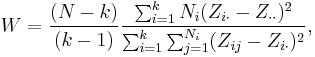Levene's test
In statistics, Levene's test[1] is an inferential statistic used to assess the equality of variances in different samples. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the null hypothesis that the population variances are equal (called homogeneity of variance). If the resulting p-value of Levene's test is less than some critical value (typically 0.05), the obtained differences in sample variances are unlikely to have occurred based on random sampling. Thus, the null hypothesis of equal variances is rejected and it is concluded that there is a difference between the variances in the population.
Procedures which typically assume homogeneity of variance include analysis of variance and t-tests. One advantage of Levene's test is that it does not require normality of the underlying data. Levene's test is often used before a comparison of means. When Levene's test is significant, modified procedures are used that do not assume equality of variance.
Levene's test may also test a meaningful question in its own right if a researcher is interested in knowing whether population group variances are different.
Contents |
Definition
The test statistic, W, is defined as follows:
where
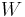 is the result of the test,
is the result of the test, is the number of different groups to which the samples belong,
is the number of different groups to which the samples belong, is the total number of samples,
is the total number of samples,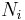 is the number of samples in the
is the number of samples in the  th group,
th group,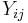 is the value of the
is the value of the  th sample from the
th sample from the  th group,
th group,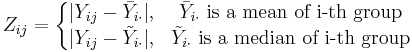
(Both definitions are in use though the second one is, strictly speaking, the Brown–Forsythe test – see below for comparison)
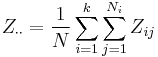 is the mean of all
is the mean of all 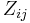 ,
,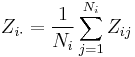 is the mean of the
is the mean of the 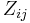 for group
for group  .
.
The significance of 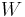 is tested against
is tested against 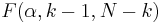 where
where  is a quantile of the F test distribution, with
is a quantile of the F test distribution, with 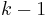 and
and 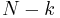 its degrees of freedom, and
its degrees of freedom, and  is the chosen level of significance (usually 0.05 or 0.01).
is the chosen level of significance (usually 0.05 or 0.01).
Comparison with the Brown–Forsythe test
The Brown–Forsythe test uses the median instead of the mean. Although the optimal choice depends on the underlying distribution, the definition based on the median is recommended as the choice that provides good robustness against many types of non-normal data while retaining good statistical power. If one has knowledge of the underlying distribution of the data, this may indicate using one of the other choices. Brown and Forsythe performed Monte Carlo studies that indicated that using the trimmed mean performed best when the underlying data followed a Cauchy distribution (a heavy-tailed distribution) and the median performed best when the underlying data followed a Chi-squared distribution with four degrees of freedom (a heavily skewed distribution). Using the mean provided the best power for symmetric, moderate-tailed, distributions.
See also
References
- ^ Levene, Howard (1960). "Robust tests for equality of variances". In Ingram Olkin, Harold Hotelling, et alia. Stanford University Press. pp. 278–292.